1-czynnikowa ANOVA
Analiza wariancji (ANOVA) dla klasyfikacji pojedynczej bada wpływ jednego czynnika klasyfikującego (podzielonego na wiele poziomów) na wartości badanej cechy mierzalnej.
Załóżmy, że mamy zbiorowości. Z każdej z nich pobrano próbę licząca elementów. Stąd łącznie mamy obserwacji.
Za pomocą jednoczynnikowej analizy wariancji testujemy hipotezę:
Wobec hipotezy alterntywnej:
Analiza wariancji wymaga spełnienia założenia normalności rozkładów we wszystkich k zbiorowościach. Dodatkowo rozkłady te powinny mieć jednakową wariancję. Zatem przed przystąpieniem do tego testu należy sprawdzić jednorodność wariancji oraz normalność rozkładów.
Podłożem analizy wariancji jest możliwość rozłożenia sumy kwadratów wariancji całościowej dla wszystkich obserwacji na sumę dwóch składników, co opisuje równanie:
Gdzie to -ty pomiar z -tej zbiorowości, to średnia z -tej próby, a to średnia ogólna z wszystkich n elementów.
Pierwszy składnik sumy opisuje zmienność wewnątrz prób. Oznaczamy go przez . Drugi składnik opisuje zmienność pomiędzy grupami. Oznaczmy go przez . wyraża wielkość odchyleń wynikających z odmienności i wpływów poszczególnych grup, podczas gdy wyraża odchylenia wynikające z wpływów przypadkowych.
W podobny sposób sumują się liczby stopni swobody, tzn.:
co możemy też zapisać:
Jeśli hipoteza zerowa jest prawdziwa, średnie kwadraty odchyleń dane wzorem:
powinny różnić się co najwyżej w granicach losowych odchyleń. Jeśli hipoteza zerowa nie jest prawdziwa, jest wyższy niż .
Średni kwadrat odchyleń pomiędzy grupami i średni kwadrat odchyleń wewnątrz grup porównujemy za pomocą statystyki Fishera , która wyraża się wzorem:
Statystyka posiada i stopni swobody. Obszar krytyczny jest obszarem prawostronnym.
Jeśli odrzucimy hipotezę zerową, nasuwa się pytanie, które z porównywanych zbiorowości się do tego przyczyniły. Należy w takiej sytuacji dokładniej przebadać różnice pomiędzy wartościami przeciętnymi w poszczególnych populacjach. Wykorzystuje się do tego testy wielokrotnych porównań (post-hoc).
TEST NIR
Istotą tego testu jest wyznaczenie tzw. najmniejszych istotnych różnic dla każdej pary oraz . Robimy to korzystając z wzoru:
Wartość odczytujemy z tablic rozkładu Studenta o stopniach swobody. Jeżeli zachodzi nierówność:
przyjmujemy, że wartości oraz różnią się istotnie.
Przykład:
Wiadomo, że związki chemiczne stosowane w leczeniu nowotworów mogą powodować obniżenie poziomu hemoglobiny we krwi (niedokrwistość).
W przypadku pewnego związku chemicznego stosowanego w leczeniu nowotworów (Lek A) podejrzewano, że przy długotrwałym stosowaniu powoduje niedokrwistość (stężenie hemoglobiny we krwi poniżej 11g/dl) w większym stopniu niż inne leki tego typu.
Do badania włączono grupę 24 osób z rozpoznaniem nowotworu. 10 z nich podawano wspomniany lek A. Pozostałym pacjentom podawano inne leki o podobnym działaniu. 7 pacjentów zażywało lek B, a 7 lek C.
W momencie przystąpienie do badania u wszystkich pacjentów poziom hemoglobiny we krwi był prawidłowy. Po zakończonej obserwacji u pacjentów ponownie wykonano morfologię krwi. Wyniki badania poziomu hemoglobiny u badanych były następujące:
| Lek A | Lek B | Lek C |
|---|---|---|
| 10,2 | 14,3 | 10,4 |
| 8,7 | 14,1 | 12 |
| 12,5 | 17 | 13,6 |
| 13,8 | 13,2 | 13,5 |
| 7,6 | 11,6 | 14,7 |
| 8,2 | 10,9 | 15,3 |
| 9,8 | 9,3 | 14,9 |
| 10,9 | ||
| 11,6 | ||
| 14,2 |
Czy pacjenci przyjmujący lek A po zakończeniu terapii mieli niższy poziom hemoglobiny we krwi niż pacjenci leczeni innymi lekami?
Aby odpowiedzieć na to pytanie wykonany jednoczynnikową analizę wariancji ANOVA.
|
Uwaga |
|
Zakładamy normalność rozkładów oraz jednorodność wariancji w grupach. W przykładzie użyto danych czysto hipotetycznych. W praktyce założenia te powinny zostać zweryfikowane. W przypadku braku pewności co do prawdziwości tych założeń w omawianej sytuacji zaleca się wykonanie nieparametrycznego testu ANOVA Kruskalla-Wallisa. |
Aby wyznaczyć wartość statystyki testowej należy wyznaczyć najpierw następujące elementy:
- średnią ogólną oraz średnie grupowe:
- sumę kwadratów odchyleń pomiędzy grupami (SSEfekt) oraz sumę kwadratów odchyleń wewnątrzgrupowych (SSBłąd):
- stopnie swobody:
- średnie kwadraty odchyleń:
Statystyka testowa dla zebranych danych przyjmie wartość:
.
Dla obliczona wartość statystyki testowej wpadnie w przedział krytyczny określony granicami .
Stąd wniosek, że poziom hemoglobiny u pacjentów stosujących różne leki różni się istotnie.
Kolejnym etapem analizy wariancji, jest stwierdzenie, które średnie różnią się między sobą (testy post-hoc). W tym celu przeprowadzimy test NIR :
- Lek A i Lek B
- Lek A i Lek C
- Lek B i Lek C
Wykonany test NIR wskazuje, że średnie poziomy hemoglobiny u pacjentów leczonych lekiem A oraz lekiem C różnią się istotnie.
Otrzymane wnioski potwierdza graficzna interpretacja zgromadzonych danych (wykres pudełkowy):
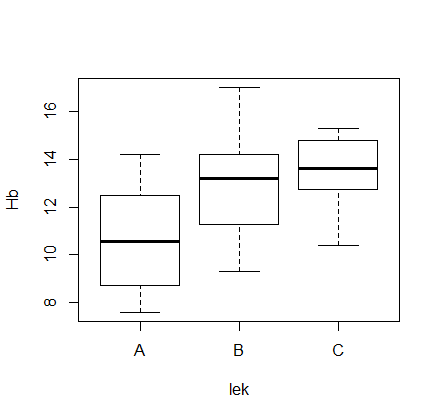
Wykres wygenerowano za pomocą programu R 2.15.2
Obok zastosowań medycznych, analiza wariancji (ANOVA) wykorzystywana jest w badaniach socjologicznych, badaniach jakości, badaniach marketingowych i wielu innych.









