Metoda k-średnich

Metoda k-średnich jest metodą należacą do grupy algorytmów analizy skupień tj. analizy polegającej na szukaniu i wyodrębnianiu grup obiektów podobnych (skupień) . Reprezentuje ona grupę algorytmów niehierarchicznych. Główną różnicą pomiędzy niehierarchicznymi i hierarchicznymi algorytmami jest konieczność wcześniejszego podania ilości skupień.

Przy pomocy metody k-średnich zostanie utworzonych k różnych możliwie odmiennych skupień. Algorytm ten polega na przenoszeniu obiektów ze skupienia do skupienia tak długo aż zostaną zoptymalizowane zmienności wewnątrz skupień oraz pomiędzy skupieniami. Oczywistym jest, iż podobieństwo w skupieniu powinno być jak największe, zaś osobne skupienia powinny się maksymalnie od siebie różnić.

Zasada działania algorytmu jest następująca:

1. Ustalamy liczbę skupień.
   Jedną z metod ustalenia ilości skupień jest umowny jej wybór i ewentualna późniejsza zmiana tej liczby w celu uzyskania lepszych wyników. Wybór liczby skupień może być oparty również na wynikach innych analiz.
2. Ustalamy wstępne środki skupień.
   Środki skupień tak zwane centroidy możemy dobrać na kilka sposobów: losowy wybór k obserwacji, wybór k pierwszych obserwacji, dobór w taki sposób, aby zmaksymalizować odległości skupień. Jedną z najczęściej stosowanych metod jest kilkakrotne uruchomienie algorytmu i wybór najlepszego modelu, gdy wstępnie środki skupień były wybierane losowo.
3. Obliczamy odległości obiektów od środków skupień.
   Wybór metryki jest bardzo istotnym etapem w algorytmie. Wpływa ona na to, które z obserwacji będą uważane za podobne, a które za zbyt różniące się od siebie. Najczęściej stosowaną odległością jest odległość euklidesowa. Stosuje się również kwadrat tej odległości czy też odległość Czebyszewa.
4. Przypisujemy obiekty do skupień
   Dla danej obserwacji porównujemy odległości od wszystkich skupień i przypisujemy ją do skupienia, do którego środka ma najbliżej.
5. Ustalamy nowe środki skupień
   Najczęściej nowym środkiem skupienia jest punkt, którego współrzędne są średnią arytmetyczną współrzędnych punktów należących do danego skupienia.
6. Wykonujemy kroki 3,4,5 do czasu, aż warunek zatrzymania zostanie spełniony.
   Najczęściej stosowanym warunkiem stopu jest ilość iteracji zadana na początku lub brak przesunięć obiektów pomiędzy skupieniami.

Przykład

Rozpatrzmy dla uproszczenia zbiór dziesięciu obserwacji, które charakteryzują dwie cechy. Sprowadza się to do przestrzeni dwuwymiarowej, w której umieszczamy 10 punktów.

$(-1,10), (3,7), (-3,2), (-2,-1), (4,0), (6,-7), (-5,-6), (-9,2), (-5,3), (4,1), (5,10)$

Ustalmy, że chcemy nasze punkty zakwalifikować do trzech skupień. Wybierzmy losowo środki skupień: (-2,-1), (-5,3), (4,1).

Czas przejść do obliczenia odległości wszystkich punktów od środków skupień. Macierz odległości wygląda następująco: (odległości zostały zaokrąglone).

$\begin{pmatrix} 3.6 & 8.5 & 5.0 \\ 9.5 & 9.0 & 6.1 \\ 3.1 & 2.2 & 7.1 \\ 0 & 5.0 & 6.3 \\ 10 & 14 & 8.3 \\ 5.8 & 9.0 & 11.0 \\ 7.6 & 4.1 & 13.0 \\ 5.0 & 0 & 9.2 \\ 6.3 & 9.2 & 0 \\ 13.0 & 12.0 & 9.1 \end{pmatrix}$

Teraz przyporządkujemy odpowiednim elementom ich skupienia.

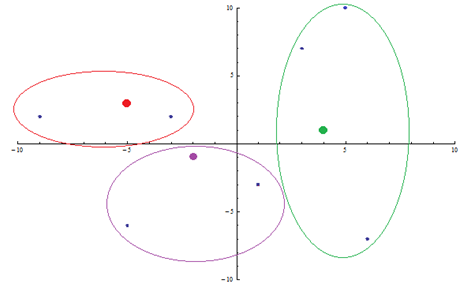
Następnie wyznaczamy nowe środki skupień przy pomocy średniej arytmetycznej. Nowe środki to $(-2, -\frac{10}{3}), (\frac{17}{3}, \frac{7}{3}), (\frac{9}{2}, \frac{11}{4})$. Kroki powtarzamy tak długo, aż zakończy się przemieszczanie punktów pomiędzy skupieniami. Algorytm kończy się po 3 iteracjach i w rezultacie dostajemy skupienia przedstawione na poniższym rysunku:

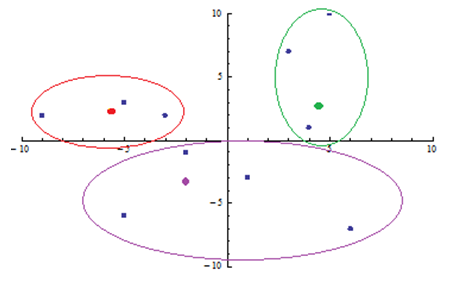
Bibliografia

[1] J. A. Hartigan and M. A. Wong (1979) "A K-Means Clustering Algorithm", Applied Statistics, 28, 100.
[2] StatSoft (2006). Elektroniczny Podręcznik Statystyki PL, Krakow, WEB: http://www.statsoft.pl/textbook/stathome.html.

AUTORZY

Kajstura Adam