Analiza koszykowa (asocjacji)
1. Wprowadzenie
Analiza koszykowa (asocjacji) służy do powiązań, skojarzeń pomiędzy konkretnymi wartościami zmiennych. Jest to szczególnie użyteczne w dużych zbiorach danych. Wysoka skuteczność tej techniki pozwala na stosowanie jej w różnych dziedzinach, szczególnie w biznesie. Aby to zilustrować, rozważmy prostą sytuację:
Klienci dokonują zakupów różnych produktów w supermarkecie. Każdy z nich komponuje własną listę zakupów. Będzie nas interesować, jakie są powiązania między kupowanymi produktami oraz przewidzeniem (z pewnym prawdopodobieństwem), jakie produkty klient może kupić mając w koszyku inne, tzn. mając zakupione np. mleko,
pytamy się, czy klient kupi także np. banany. Innymi słowy "Jakie produkty
kupowane są najczęściej razem".
Analiza koszykowa jest w stanie odpowiedzieć nam na te pytania. Takiej analizie jest poddawany każdy z nas -
robiąc właśnie między innymi zakupy w marketach. Każdy paragon ma swój unikalny numer ID i widnieje na nim lista
artykułów, które podlegają analizie. Wynikiem analizy koszykowej są reguły asocjacji postaci:
JEŚLI [poprzednik] to [następnik]
Zanim przejdziemy do przykładu ilustrującego analizę asocjacji, podamy kilka podstawowych parametrów, aby
jego zrozumienie było prostsze.
Krótko o wzorach
Podamy krótkie wyjaśnienie podstawowych i najważniejszych współczynników w analizie koszykowej.
- wsparcie reguły - jest to odsetek transakcji, które zawierają wybraną regułę. Istotne jest to, że wsparcie jest liczbą z przedziału [0,1].
- zaufanie - zwane też pewnością reguły, jest to odsetek transkacji zawierających analizowaną regułę w zbiorze tych, które spełniają poprzednik danej reguły. Wielkość ta również należy do przedziału [0,1] - odpowiada bowiem odpowiedniemu prawdopodobieństwu warunkowemu.
- przyrost - jest z kolei miarą, która określa nam, czy fakt wystąpienia jednego produktu wpływa na zwiększenie prawdopodobieństwa wystąpienia drugiego w ramach jednej transkacji. Współczynnik ten jest oczywiście dodatni.
Teraz, w ramach utrwalenia przyjrzyjmy się wzorom na te 3 wielkości.

Czasem używamy dodatkowo parametru korealcja, który określa, w jaki sposób fakt, że klient wybrał produkt A, zwiększa lub zmniejsza prawdopodobieństwo, że wybierze on również produkt B (jest to zatem szerzej rozumiany przyrost). Korelację wyrażamy poprzez iloraz
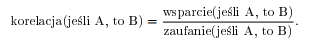
Jeśli przyjmuje ona wartości większe od 1, to mamy do czynienia z pozytywną korelacją. W przeciwnym wypadku możemy mówić o negatywnej korelacji. Możemy teraz przejść do krótkiego przykładu, który zobrazuje te teoretyczne podstawy zagadnienia analizy koszykowej.
Przykład
W celu wykonania interesującej nas analizy wykorzystamy program Statistica. Skorzystamy z gotowego arkusza o nazwie MarkeBasket10percent. Aby rozpocząć naszą analizę wchodzimy w moduł Data Mining i zaznaczamy opcję Analiza koszykowa. Jak przy każdej analizie, otrzymujemy okienko, w którym musimy wybrać interesujące nas zmienne. W bloku Zmienne wielokrotnych odpowiedzi wybieramy wszystkie zmienne prócz dwóch pierwszych, pownieważ zawierają one tylko numer i datę transakcji, a to oczywiście nie podlega analizie. Po wyborze zmiennych przechodzimy na kartę Więcej i ustalamy minimalne wsparcie, zaufanie oraz korelację na poziom 0,1, ponieważ bardzo rzadko te wielkości przekraczają domyślnie ustawiony poziom.1 Po ustawieniu tych parametrów przechodzimy dalej i otrzymujemy wyniki. W okienku możemy wygenerować sobie rysunki sieci reguł, nas jednak interesuje poszukiwanie reguł. Po kliknięciu na reguły otrzymujemy wyniki analizy.
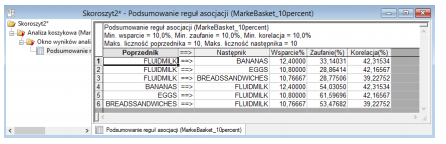
Udało się zatem znaleźć kilka reguł. Widzimy na przykład, że ludzie, którzy kupowali mleko, częściej sięgali po banany niż jajka. Odpowiednie prawdopodobieństwa wynoszą kolejno 33,1% oraz 28,9%. To tylko jeden, przykładowy wniosek. Możemy poszukiwać tego typu reguł i zmieniać poziom minimalnego wsparcia, zaufania oraz korelacji. Program oferuje nam również określenie maksymalnej liczby elementów poprzednika i następnika. Podsumowując, jest to zabawa na wiele godzin, która pozwala wyciągać ciekawe wnioski! Resztę zostawiamy Czytelnikowi!
Literatura
[1] basket.pdf
[2] ekonomia.wne.uw.edu.pl/ekonomia/getFile/372
AUTORZY:
Krystian Kaczmarek
Absolwent Wydziału Matematyki Stosowanej Politechniki Śląskiej w Gliwicach, matematyk o specjalizacji matematyka finansowa. Wśród jego matematycznych zainteresowań prócz statystyki znajdują się zagadnienia analizy matematycznej: rachunek całkowy i różniczkowy, algebry oraz geometrii. Adam Kajstura: Absolwent matematyki na Politechnice Śląskiej w Gliwicach. Marta Kwapulińska: Absolwentka kierunku matematyka Politechniki Śląskiej w Gliwicach.









