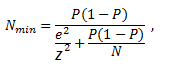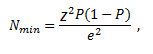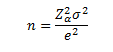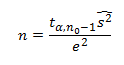Badanie o charakterze częściowym to badanie statystyczne, w którym o rozkładach cech statystycznych dla całej populacji wnioskuje się w oparciu o rezultaty badań przeprowadzonych na pewnej podgrupie populacji generalnej (próbie). Metoda reprezentacyjna jest najbardziej prawidłową realizacją badania częściowego, w której próba dobierana jest w sposób losowy.
W celu pozyskania informacji o rozkładach cech statystycznych w populacji generalnej, wybiera się w sposób losowy grupę jednostek, czyli próbę, na niej zaś przeprowadza się badania mające na celu wyznaczenie analogicznych rozkładów. Otrzymane rezultaty służą do wnioskowania o całości populacji, przy czym wnioskowanie to jest obarczone błędem. Rachunek prawdopodobieństwa pozwala na oszacowanie wartości tego błędu.
Istotnym aspektem metody jest dobór próby. Ponieważ na jej podstawie wnioskujemy o całej populacji generalnej, chcemy, aby próba stanowiła dobrą (w sensie zachowania właściwości i prawidłowości) reprezentację całości. Najważniejszymi czynnikami, które mają wpływ na dokładność metody reprezentacyjnej są: struktura zbiorowości, wykorzystany schemat losowania oraz liczebność próby.
Istnieje możliwość wyznaczenia minimalnej liczebności próby w oparciu o określone parametry (m.in. dotyczące jakości wyników badania). Do tych parametrów należą:
- Szacowana wielkość frakcji, czyli odsetek jednostek spełniających określoną cechę;
- Maksymalny błąd oszacowania;
- Poziom istotności, który interpretuje się jako prawdopodobieństwo, z jakim popełniony zostanie błąd oszacowania o zadanej wartości maksymalnej;
- Liczebność populacji generalnej (dla populacji skończonej).
Minimalną liczebność próby wyznacza się inaczej, w zależności od tego, czy mamy do czynienia z populacją skończoną, czy nieskończoną. Z populacją nieskończoną rzadko mamy do czynienia w praktyce. W niektórych sytuacjach wygodniej jednak traktować populację o skończonej liczbie jednostek jako populację nieskończoną (w szczególności kiedy liczebność populacji generalnej jest bardzo duża). Dla populacji skończonej wzór na minimalną liczebność próby ma następującą postać:
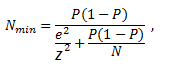
natomiast dla populacji nieskończonej:
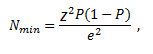
gdzie:
P – szacowana wielkość frakcji,
z – wartość wynikająca z przyjętego poziomu istotności (α), obliczana przy pomocy dystrybuanty rozkładu normalnego,
N – liczebność populacji generalnej (w przypadku populacji skończonej),
e – maksymalny błąd oszacowania.
Jeżeli nie jesteśmy w stanie oszacować wielkości frakcji P, jej wartość powinna zostać ustawiona na 50% (domyślnie).
Ponieważ rozważamy liczebność populacji, otrzymany wynik powinien być liczbą naturalną. Dlatego też wartość będąca wynikiem obliczeń zaokrąglona jest w górę. Mamy wówczas pewność, że wyniki badania przeprowadzonego na próbie o liczności nie mniejszej niż minimalna liczebność próby będą spełniały założenia, które zostały nałożone poprzez zadane parametry (maksymalny błąd oszacowania i poziom istotności).
Kalkulator wielkości próby pozwala na wyznaczenie minimalnej liczebności próby, dzięki której uzyskamy wyniki badania z zadaną dokładnością. Kalkulator jest dostępny w dwóch wariantach: dla populacji skończonej i dla populacji nieskończonej.
Przykład:
Chcemy przeprowadzić kontrolę jakości partii liczącej 10000 konserw. Jedynym sposobem na wskazanie ze stuprocentową pewnością dokładnej liczby puszek, których zawartość jest niezdatna do spożycia, jest otwarcie każdej konserwy w partii. Jest to oczywiście rozwiązanie niedopuszczalne; dlatego chcemy otworzyć taką liczbę puszek, aby prawdopodobieństwo tego, że faktyczny odsetek uszkodzonych konserw w całej partii będzie się różnił od oszacowanego o więcej niż 4%, wynosiło 0,05. Równoważnie: chcemy mieć 95% pewności, że rzeczywisty odsetek uszkodzonych konserw nie różni się od oszacowanego na podstawie próby o więcej niż 4%.
Aby uzyskać wyniki z opisaną wyżej dokładnością powinniśmy otworzyć 566 puszek.
Określenie minimalnej liczebności próby dla średniej:
W podobny sposób możemy określać minimalną liczebność próby dla szacowania średniej. Liczebność próby zapewniającą uzyskanie ustalonej z góry dokładności estymacji przedziałowej średniej wyraża wielkość:
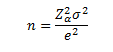
Należy jednak pamiętać, że stosowanie tego wzoru wymaga normalności rozkładu badanej zmiennej oraz stałej i znanej wariancji σ2.
Jeżeli populacja generalna ma rozkład normalny z nieznaną wariancją σ2, minimalną liczebność próby możemy wyznaczyć korzystając z tzw. dwustopniowej metody Steina. Liczebność próby określamy wtedy na podstawie wzoru:
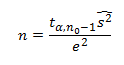
Gdzie:
n0 – liczebność próby w badaniu pilotażowym,
S2 wariancja próby obliczona na podstawie badania pilotażowego,
tα,n-1 – wartość odczytana z tablic rozkładu t-Studenta dla n0-1 stopni swobody.
Przykład:
Niezbędna liczebność próby przy szacowaniu średniej w populacji może poinformować na przykład jak liczna powinna być próba, żeby móc na jej podstawie oszacować średnią wagę ogółu noworodków przy ustalonym poziomie istotności α=0.01 i maksymalnym błędzie szacunku 0.3kg, jeżeli jej rozkład jest normalny ze znaną wariancją 0.56.
W tym przypadku szukana liczba to 42, co oznacza, że próba musiałaby zostać przeprowadzona na co najmniej 42 noworodkach.