Analiza skupień

Analiza skupień obejmuje algorytmy służące do pogrupowania obiektów w taki sposób, aby stopień powiązania elementów z tej samej grupy był jak najwyższy, a z elementami z innych grup jak najniższy.

Algorytm AGNES

Algorytm AGlomerative NESting należy do metod aglomeracyjnych, co oznacza, że każda obserwacja początkowo traktowana jest jak osobny klaster. W kolejnych etapach grupy podobne do siebie łączone są w coraz większe grupy tak długo, aż nie powstanie klaster obejmujący wszystkie elementy.

Załóżmy, że mamy n elementów określonych przez k zmiennych mierzalnych.

Krok 1 – standaryzacja zmiennych

Jeśli zmienne opisujące obiekty są wyrażone w innych miarach lub jednostkach bądź zróżnicowanie obiektów pod względem poszczególnych cech nie jest jednakowe (różne odchylenia standardowe) niezbędna jest standaryzacja zmiennych. Unormowania zmiennych dokonujemy za pomocą wzoru:

$z_{ij}= \frac{x_{ij}-\overline{x_j}}{s_j},~~~~j=1,..., k,~~~~i=1, ..., n.$

Krok 2 – macierz odległości

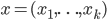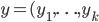Następnie tworzymy macierz odległości D pomiędzy rozpatrywanymi elementami. Odległości obliczamy traktując wektor wartości kolejnych zmiennych opisujących dany obiekt jako punkt przestrzeni k-wymiarowej. Najpowszechniej używaną miarą odległości jest odległość euklidesowa, która dla dwóch punktów   $x=(x_1,\ldots,x_k)$ oraz $y=(y_1,\ldots,y_k$ wyrażona jest wzorem:

$d(x,y)=\sqrt{\sum\limits_{j=1}^k (x_j-y_j)^2}$

Krok 3 – znalezienie obiektów najbardziej podobnych

Na podstawie macierzy odległości D znajdujemy dwa obiekty, dla których dzieląca je odległość jest najmniejsza. Obiekty te utworzą pierwszy klaster, który w dalszych krokach traktowany będzie jako pojedynczy obiekt.

Krok 4 – środek ciężkości

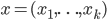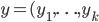Współrzędne nowego klastra określamy jako środek ciężkości współrzędnych opisujących dwa połączone obiekty. Środek ciężkości dla dwóch punktów $x=(x_1,\ldots,x_k)$ oraz $y=(y_1,\ldots,y_k$ wyznaczamy za pomocą wzoru:

$(\frac{x_1+y_1}{2}, ..., \frac{x_k+y_k}{2})$

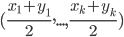
Krok 5 i kolejne

Kroki 2, 3 oraz 4 powtarzamy do momentu uzyskania jednego skupiska łączącego wszystkie rozpatrywane obiekty.