2-czynnikowa ANOVA
Analiza wariancji (ANOVA) dla klasyfikacji podwójnej bada wpływ dwóch czynników klasyfikujących (podzielonych na wiele poziomów) na wartości badanej cechy mierzalnej.
Jeśli w każdej podgrupie utworzonej poprzez jednoczesny podział oby czynników na poziomy znajdują się przynajmniej 2 obserwacje, badamy także wpływ interakcji rozpatrywanych dwóch cech na zmienność cechy mierzalnej.
Niezbędnymi założeniami analizy wariancji jest normalność oraz jednorodność wariancji w podgrupach wyznaczonych przez poziomy czynników klasyfikujących.
Zwykle zzynniki klasyfikujące oznaczmy wielkimi literami alfabetu łacińskiego: A, B, AB (interakcja), natomiast ich poziomy małymi: a, b, ab.
Zakładać będziemy, że we wszystkich podgrupach wyznaczonych przez czynniki klasyfikujące znajduje się taka sama liczba obserwacji k.
Za pomocą dwuczynnikowej analizy wariancji testować będziemy zestaw hipotez:
Źródło zmienności A nie różnicuje wyników.
Źródło zmienności B nie różnicuje wyników.
Źródło zmienności AB nie różnicuje wyników.
Każde źródło zmienności będziemy testować osobno. W tym celu niezbędne jest wyznaczenie dla każdego źródła liczby stopni swobody , sumy kwadratów odchyleń , średniego kwadratu odchyleń oraz wartości statystyki testowej , która przy założeniu prawdziwości hipotezy zerowej ma rozkład F Snedecora o liczbie stopni swobody odpowiadających liczbie stopni swobody analizowanego źródła oraz błędu (czynnika losowego).
Parametry te obliczamy korzystając z następujących wzorów:
| Źródło zmienności (Z) | (liczba stopni swobody) | (suma kwadratów odchyleń) | (średni kwadrat odchyleń) | (statystyka testowa) | (wartość krytyczna odczytana z tablic) |
|---|---|---|---|---|---|
| A | |||||
| B | |||||
| AB (interakcja) | |||||
| Błąd (e) | |||||
| Całość |
Oznaczenia:
- - ilość obserwacji dla pojedyńczej kombinacji wyznaczonej przez poziomy czynników klasyfikujących,
- - średnia z wszystkich obserwacji,
- - średnia obserwacji na i-tym poziomie cechy A,
- - średnia obserwacji na j-tym poziomie cechy B,
- - średnia obserwacji należących do i-tej kategorii cechy A i j-tej kategorii cechy B,
- - wartość pojedyńczej obserwacji.
Jeśli dane źródło zmienności nie różnicuje wyników, oczekujemy, że wartości nie będą odchylać się od średniej bardziej niż w granicach błędu. Dlatego też efekt danego czynnika porównujemy z działaniem czynnika losowego (Błąd).
Jeżeli dla ustalonego wartość krytyczna jest mniejsza od wyliczonej wartości statystyki testowej , odrzucamy hipotezę zerową na rzecz hipotezy alternatywnej głoszącej, że źródło zmienności różnicuje wyniki.
Przykład - Wpływ stosowanego leku oraz prowadzonej fizjoterapii na ogólną ocenę aktywności choroby (wg skali VAS) u pacjentów z reumatoidalnym zapaleniem stawów.
Pacjentów z reumatoidalnym zapaleniem stawów poproszono o ogólną ocenę stanu zdrowia w skali od 0 do 100, gdzie 0 oznacza bardzo dobre samopoczucie, a 100 bardzo złe samopoczucie. Do badania włączono 30 pacjentów, którzy aktywność choroby oceniali w granicach 70-80.
W sposób losowy wybrano po 10 pacjentów, którym podano Lek I, Lek II oraz placebo. Z każdej 10 wybrano (na drodze losowania) 5 chorych, u których równocześnie prowadzono fizjoterapię.
Uwaga:
W praktyce zaleca się wykonywanie testu na większej ilości obserwacji. Istnieje wtedy możliwość weryfikacji jednorodności rozkładów w podgrupach.
W omawianych przykładzie rozpatrujemy małą grupę chorych w celu przejrzystego przedstawienia sposobu wykonywania obliczeń. Czytelnik powinien mieć jednak na uwadze, że przytoczony przykład stanowi jedynie przykład poglądowy.
W przypadku większej ilości obserwacji zaleca się skorzystaniem ze statystycznych programów komputerowych, np. Statistica, R.
Po miesiącu terapii chorych poproszono o ponowne dokonanie oceny samopoczucia. Otrzymano następujące wyniki:
|
|
Placebo |
Lek I |
Lek II |
|
Prowadzono fizjoterapię |
60, 54, 88, 76, 72 |
48, 73, 39, 35, 51 |
43, 67, 53, 48, 49 |
|
Nie prowadzono fizjoterapii |
90, 87, 67, 55, 82 |
56, 76, 62, 44, 52 |
57, 75, 78, 64, 82 |
Czy na ocenę samopoczucia pacjentów miały wpływ:
- rodzaj przyjmowanego leku,
- fizjoterapia,
- współdziałanie fizjoterapii i przyjmowanego leku?
Pierwszy z rozważanych czynników (podawany lek) dzieli się na 3 poziomy – Lek I, Lek II oraz placebo, dlatego liczba stopni swobody dla tego źródła zmienności wyniesie 2.
Aby obliczyć sumę kwadratów odchyleń dla rodzaju leku, najpierw musimy wyznaczyć średnie w poszczególnych grupach:
Analogicznie obliczamy dwie pozostałe średnie:
oraz średnią ogólną:
.
We wszystkich rozważanych kombinacjach ilość obserwacji jest równa 5.
Suma kwadratów odchyleń oraz średni kwadrat odchyleń wyniosą odpowiednio:
Wykonując analogiczne obliczenia dla wszystkich źródeł zmienności otrzymamy wyniki, jakie przedstawia tabela:
| Lek | 2 | 1921,7 | 960,8 | 6,1 | 3,40 |
| Fizjoterapia | 1 | 974,7 | 974,7 | 6,1 | 4,26 |
| Lek i Fizjoterapia (interakcja) | 2 | 236,6 | 118,3 | 0,7 | 3,40 |
| Błąd (e) | 24 | 3810,4 | 158,8 | ||
| Całość | 30 |
W obliczeniach przyjęliśmy .
Zebrane w tabeli wyniki jednoznacznie wskazują, że czynnikami różnicującymi ocenę samopoczucia pacjentów są przyjmowany lek oraz prowadzona fizjoterapia. Nie stwierdzono natomiast istotnego wpływu interakcji tych dwóch czynników na ocenę stanu zdrowia pacjenta.
Oceny poszczególnych czynników możemy przedstawić także graficznie. Na wykresie przedstawiono średnie wartości ocen stanu zdrowia pacjentów względem stosowanego leku oraz prowadzonej fizjoterapii. Pozioma linia wyznacza średnią ogólną wszystkich pomiarów.
Zebrane dane wskazują, że swoje samopoczucie najlepiej oceniali stosujący Lek I, a najgorzej dostający placebo.
Pacjenci, u których prowadzono fizjoterapię, niżej oceniali aktywność choroby, niż pacjenci, u których jej nie prowadzono.
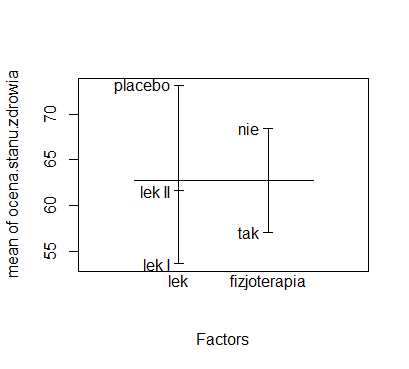 Wykres wygenerowano za pomocą programu R 2.15.2
Wykres wygenerowano za pomocą programu R 2.15.2
Z kolei analizując wykres dla interakcji możemy stwierdzić, czy wpływ poszczególnych źródeł zmienności jest addytywny (niezależny od siebie) czy też istnieje wpływ interakcji (wynikowa wartość badanej cechy mierzalnej nie jest prostym złożeniem efektów jaki wywołuje każdy czynnik z osobna).
W pierwszym przypadku krzywe na wykresie interakcji powinny być równoległe. Natomiast w przypadku występowania interakcji krzywe powinny mieć istotnie różnie nachylenia.
W omawianym przykładzie krzywe nie są równoległe. Największe zróżnicowanie wyników powodowane prowadzeniem jednoczesnej fizjoterapii obserwujemy u pacjentów, którzy stosowali lek II. Jednak różnica ta nie powoduje istotnych różnic w nachyleniu krzywych. W wyniku przeprowadzonej analizy wariancji nie stwierdzono wpływu interakcji tych dwóch czynników.
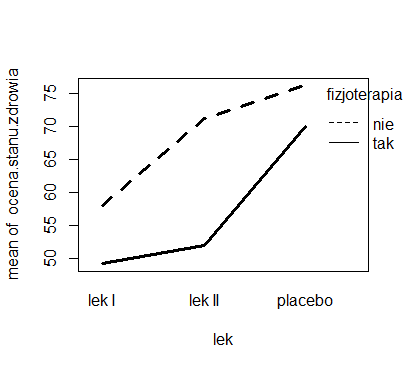 Wykres wygenerowano za pomocą programu R 2.15.2
Wykres wygenerowano za pomocą programu R 2.15.2









